Are Aghion and Howitt Right About Competition and Innovation?

Some reasons to doubt the recent Nobel Prize winners

Philippe Aghion and Peter Howitt have just won the Nobel Prize in economics, largely on the basis of one paper. In “A Model of Growth Through Creative Destruction”, they capture the constant churn of the market, and show how it can deliver sustained growth through innovations.

Aghion-Howitt (1992) makes very specific claims about the relationship between competition and innovation. Rather than growth monotonically increasing as firms get closer to monopoly, growth comes fastest when we are at an intermediate level of competition. I want to put this to the test. I find the theory convincing, and gesturing at something important. However, the empirical support is incredibly paltry. Contrary to the frequent assertions of Aghion and partisans, it has not been decisively and repeatedly proved.

First, though, a brief history of growth theory. We begin in earnest with Robert Solow (1956), who writes down a production function for the economy where output Y is a function of capital and labor. Labor is exogenously given by population growth, and capital is determined by savings relative to a rate of depreciation on capital. Since the production function will exhibit diminishing marginal returns to capital, eventually economic growth will peter out, and we will be in a steady state level of per capita output.

The model can be extended simply by including additional factors of production – for instance, in Mankiw-Romer-Weil (1992), they include human capital as an explanatory variable. We could also include land, if we wanted – it gives us a simple way to attribute growth to different causes. The part that we cannot explain is taken to be technological growth, and is a scalar A which multiplies the effective productivity of labor.

It is, nevertheless, unsatisfactory for a few reasons, the most important of which is that it lacks a theory of technological change. The residual A which we multiply the production function by is just exogenously given. When making predictions, we would like to do better than just assume that a constant rate of growth will prevail forever. People seek to discover ideas because doing so is profitable, not because they fall to us from the skies.

Paul Romer is the first to soundly model it, first in 1986 with the AK model, and in 1990 with “Endogenous Technological Change”. Things in Romer’s world are produced with a combination of ideas and stuff. Since ideas require a fixed cost to find but are thereafter free, the economy exhibits increasing returns to scale. Growth comes from increasing varieties – we have a taste for variety and are in Dixit-Stiglitz world. We don’t get infinite growth in finite time because none of the people can collect the full marginal return to their inventive activity, so we have a suboptimally low level of invention. It is possible for no growth to ever occur, if the rate of return on invention falls below the rate of interest, and countries need not have any tendency to converge if information does not flow across national boundaries.

In contrast to Romer, Aghion and Howitt does not have everyone necessarily benefit from innovation. In fact, it is entirely possible for there to be too much innovation, when firms invest in finding ideas to displace their rivals at the expense of simply producing useful output. Aghion and Howitt’s model has a two period structure, with each period starting when a new invention arrives. The rate at which they arrive is determined by the amount that people invest into finding new ideas. Whenever a new idea is found, the firm takes the whole market until a competing firm discovers a new idea to surpass them.

As noted at the beginning, these models make predictions. The point of a model is not to reason from axioms to discover a priori truth, but rather to fit the facts through the underlying processes as simply and tractably as possible. Specifically, they predict that there will be an inverted-U curve between competition and innovation. At the very highest levels of competition, the gains from a new discovery will be eaten away by other firms investing. In the case of monopoly, there is no reason to invest in finding a new idea, since you already have the whole market. In between, there is the fastest rate of technological discovery.

The empirical paper most commonly cited by Aghion is Aghion, Bloom, Blundell, Griffith and Howitt (2005), which posits an inverted-U curve of competition and innovation. Their sample is all the firms beginning A through L on the London Stock Exchange, plus major R&D firms. (Why this curious sample? Nicholas Bloom explains that this was before any easy method to match firms with patents, and simply doing this took three months. A-L corresponded with the divisions in one of the two books listing out information for all firms on the London Stock Exchange. I don’t think that this is a serious problem with the paper.)

They measure market competition with the Lerner index, which is price minus marginal cost, divided by price. Here it is operating profit minus a financial cost for capital depreciation and cost of capital taken to be fixed across all firms. They normalize perfect competition to one by setting

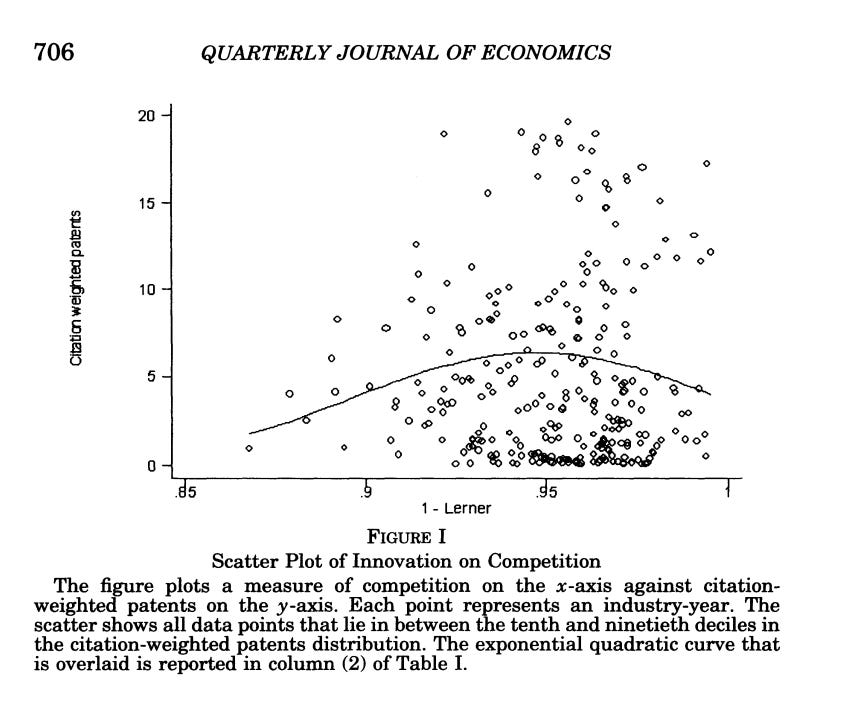
I would like to first say some things the paper did right. It did not use concentration as a proxy, which would have made for a meaningless regression. It does try and use profit margins, deducting the presumed fixed costs. There are, however, a few problems with this paper. The main one is just the central regression, though. On the Y axis are citation weighted patents, on the X axis is the Lerner index, where the further right you go the more competitive things are. A quadratic curve is an ambitious curve to fit!

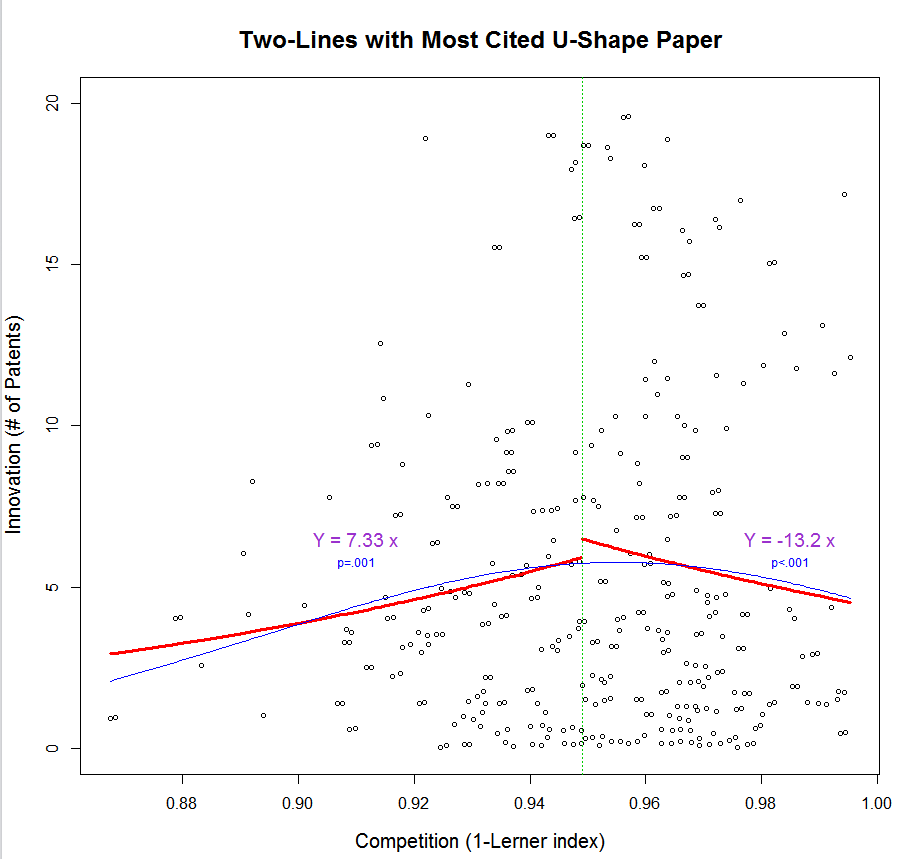
I just cannot seriously look at the central regression chart and say “yes, the inverted-U shape relationship is robustly shown.” But that is what they claim in their paper! The best case for the paper is that when you divide it up, the slope of two linear regressions do change. (I take this from a DataColada post). Still, it does not inspire confidence.

These are just the estimates without instrumental variables. Their sources of exogenous variation here are differences in when the industry was exposed to regulatory actions which increased competition, as well as the exposure of everyone to the single market for trade with Europe. (The last is essentially a shift-share, where there were differences in trade barriers before they were all reduced to 0 at a stroke. The details can be found in the working paper version). But, I really hope I’m going crazy here – shouldn’t we be clustering standard errors here? Even after two-way fixed effects for industry and year – which is basically subtracting out the average for the industry over time, and then for that year in particular – shocks to a particular industry in a particular year will last over time. A discovery in 1988 could lead to more discoveries in that vein later on. Failing to cluster will lead to too many observations, and for you to spuriously reject the null hypothesis. This can be easily seen by considering what would happen if you looked at patents every minute, or patents every second, and treated each as an independent observation. What this also means is that the instrumental variable will cause an effect on the outcomes in the year it happens, and then persistently after, such that it breaks two way fixed effects.

Another serious problem is that we only have information on firms which are on the stock market. We do not have information on their competitors. It hardly makes sense to speak of the competitiveness of the industry when we observe only part of it.

I am also suspicious of their measure of competition. Measuring marginal cost is really hard. I have seen it described as the equivalent of house-to-house fighting. We do not have a simple rubric for just finding it. Just assuming that the cost of capital is the same in all industries is surely not correct.

In addition, a low rate of profit is perfectly consistent with market power if firms are not profit maximizing for their shareholders. This can be easily achieved by agency problems. Suppose firms in uncompetitive industries spend more of their rents on management and labor. This doesn’t seem implausible to me at all – do we not hear all the time about companies which have grown indolent from a lack of competition?

Another reasonable concern is that patents are not the best proxy for innovation here. Many innovative ideas, in particular process improvements, are never patented. Patents are the best proxy we have for innovation at the moment, and using them is reasonable, but we might be concerned that the choice to patent or not patent an item is itself endogenous to market competition. For instance, suppose that companies in tighter competition acquire patents to defend their ideas, while companies facing little competition choose to keep their ideas a secret instead. Companies which face the strongest competition do not innovate, so they neither patent nor innovate. In such a world, we would get a spurious U-shape.

So what about the other evidence than this? It’s the same sort of muddle. There are papers which find an inverted U. There are papers which do not find an inverted U. Everything in this literature doesn’t publish well, because it’s all fundamentally kinda shabby. We’re trying to fit regression curves on not many observations with poor knowledge of both our x and y variables in a sample which is selected in ways we do not understand. The most recent literature review that I can find is here; readers braver than I are welcome to sort through the papers mentioned.

I’ve seen enough to make conclusions. I do not think that the inverted U of competition and innovation is remotely proven, much less conclusively proven as Aghion has stated many times. What this does strongly argue for, however, is that monopolies are not particularly great for innovation, which does strongly contradict the Romer view of profits being a sufficient statistic for innovation. There is a lot of evidence that total factor productivity is higher when there is more competition, for reasons that are not always clear. I am similarly inclined to believe that competition is good for innovation too.