Endogenous Growth and Human Intelligence

How a small change in assumptions leads to enormously different conclusions

i. Why model?

Why do economists model? Why are we so insistent on boiling our thoughts down into a tidy sequence of equations? A model of the world is not intended to be a one-for-one representation of the world, nor could it be. Rather, the point is to direct our estimation. If we can boil down the world into a few parameters, we can then *estimate* those parameters. Empirics without theory would be feeling the world in darkness — we are more likely to lead ourselves astray than find the truth. 

The problem with the macro growth literature is that one doesn’t know where to start. It is a long sequence of ideas, and bringing up any part of it necessitates mentioning preceding parts. So let us start at the beginning, and, while not implying that there are uninteresting facets of economics, proceed as fast as we can to the very interesting parts. :)

ii. The History of Macroeconomic Growth Models

Macro growth models start in earnest with Solow, who connected capital accumulation to growth. Capital is taken to have diminishing marginal returns, in contrast to the cruder Harrod-Domar model. There exists a rate of savings which maximizes long run consumption, and given a particular technology set consumption will reach a constant level. (This rate of savings is called the Golden Rule level of savings, after Phelps). We assume perfect competition in production. (Monopoly distortions can be subtracted from the steady state level of consumption). Initial conditions have no effect on the long run rate, which is the same for all places and much lower than our present living standards. It is therefore necessary to invoke technological change, which is taken to be growing at an exogenously determined rate. As Arrow wrote, “From a quantitative, empirical point of view, we are left with time as an explanatory variable. Now trend projections … are basically a confession of ignorance, and what is worse from a practical viewpoint, are not policy variables”

The formulas are simple and clean, and you can make meaningful predictions about growth rates. Still, this clearly does not very well describe the world. There are large differences in per capita income across the globe. If there are diminishing marginal returns to capital, and that is all that matters, then capital should be flowing from developed countries to developing countries. It isn’t. In fact, more skilled people (who can be thought of as possessing a kind of capital, human capital) immigrate to more skilled countries! (Lucas 1988). Even if there are bars to capital flowing between countries, no such barriers between southern and northern states in the US. Barro and Sala-i-Martin (1992) found that, with reasonable parameters, the return to capital should have been five times higher in the South in the 1880s. Yet, most capital investment took place in New England states. 

The bigger problem is that it predicts that growth rates should be declining over time. They are not. If anything, they are increasing over time. Even if the growth rate is constant and positive, that implies that the absolute value of growth is increasing over time. Appending human capital to the model can allow you to estimate the contribution of skills, in contrast to just tools and resources, but it is just a subset of capital and won’t lead to unbounded growth.

Enter Romer (among others). The value of human capital is not just ability, it is ideas. Ideas are non-rivalrous, and largely non-excludable. (That is, someone using an idea does not make it unusable by another). You must drop the assumption of perfect competition as a result, as perfect competition requires goods to be perfectly divisible. Dropping the assumption of perfect competition leads to far-reaching changes – it is now possible for firms to earn excess profits, which makes investing into new production technologies worthwhile.

The idea seems incredibly obvious. Why was it so long delayed? The first problem is that no tractable model of monopolistic competition existed until the mid-70s, when Dixit-Stiglitz was published. The second, deeper problem is that if finding new ideas leads to finding ideas faster, the model actually predicts infinite growth in finite time. There is no equilibrium. 

This is like a bug in your code leading to an overflow error. The derivative of the technology set A is equivalent to -A to the power of some number, represented with the greek letter phi. If phi is greater than one, growth is infinite in finite time; if it is less than one, growth eventually stops; and if it happens to be exactly one, then technological progress is back to being totally unaffected by other progress, and we’re back in the neoclassical world of the Solow model. This sort of knife edge equilibrium is to be avoided. Early takes on endogenous growth, like Nordhaus’s 1969 paper, had to resort to an endogenously determined knowledge variable clumsily mashed to an exogenous growth of knowledge variable. The world called out for 

By the 80s, it was an idea whose time had come, and after Romer came a small boom in models. (I hope you can forgive me for not having read all of them). I shall deal mainly with Romer 1986 and Romer 1990, but wish to mention Aghion-Howitt 1991, in which the bounding on growth is provided by anticipated future creative destruction. People invest in finding knowledge, which replaces past companies. Because people know their work may be replaced, so their investment into research is bounded.

In Romer 1986, humans invest in finding knowledge, which is added to a non-depreciating stock. Production of a single consumption good is globally convex with respect to knowledge — that is, it exhibits increasing returns as you get more and more knowledge. There are diminishing returns in investing to find knowledge, which means there is a finite rate of growth which is the optimum achievable. In this model, you keep the assumption of perfect competition.

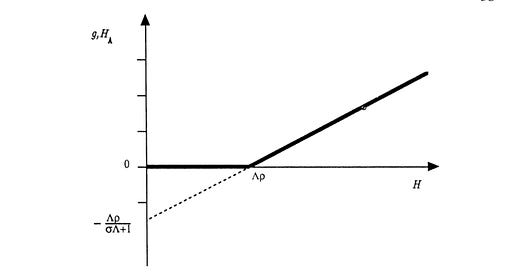
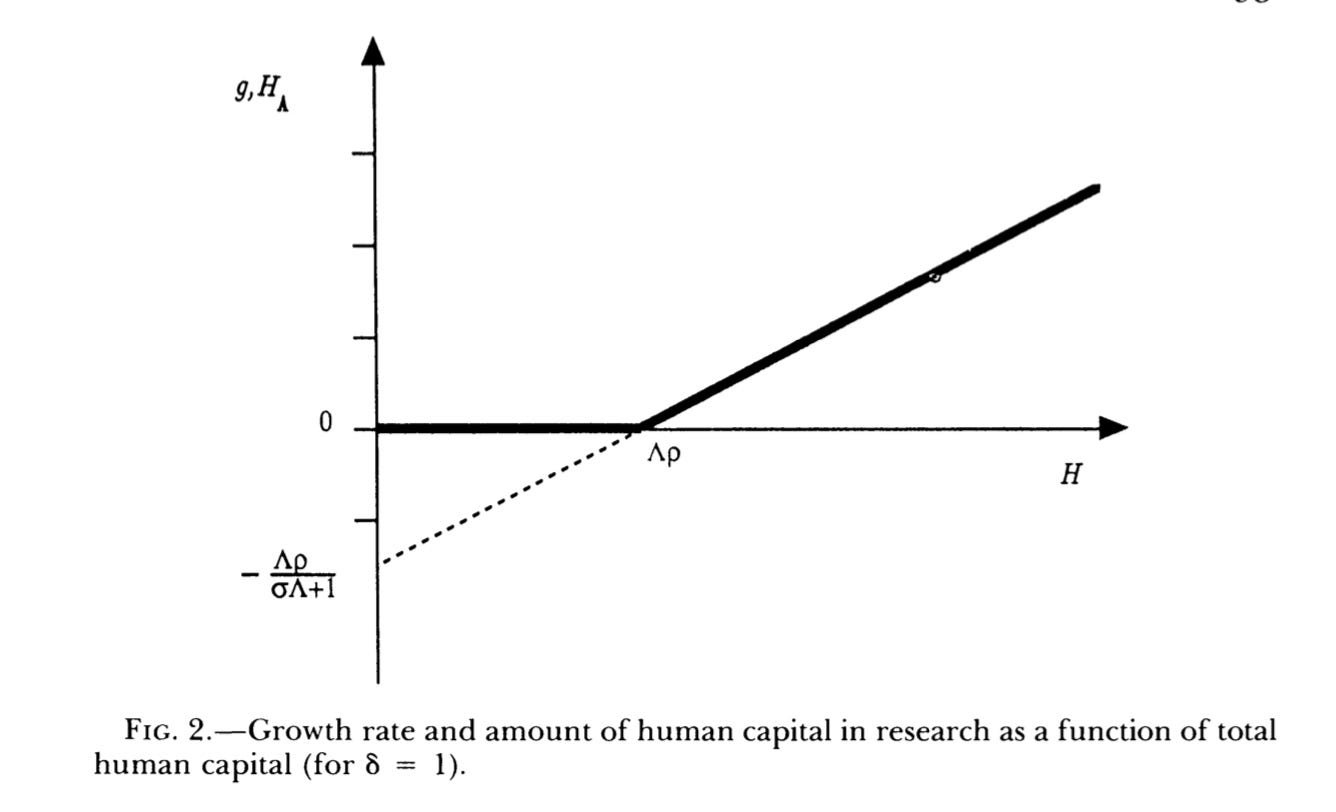
Romer 1990 drops the assumption of perfect competition. Because each good is only partly excludable, it isn’t possible for there to be a universe of price-taking firms. Firms only get a part of what they make, but there are increasing returns to investment socially, similar to 1986. People choose between producing now, and investing in research, which pays off later. In an extreme case, a sufficiently low level of human capital means that all payoffs from investing will be less than the discount rate, and no growth occurs. Because of the increasing returns, countries can get to wildly different outcomes from relatively small differences in initial levels of human capital. (This is illustrated in the image below)

.

In both papers, Romer treats human capital as being essentially similar to physical capital. People are born with none, and it is only with investment and training that we acquire any. This means that technological progress is invariant to population size — only the total stock of human capital matters. This is why an expansion of trade to another nation will increase the rate of technological discovery, but increasing the population of a country won’t. It is for exactly the same reason that doubling the population would not increase physical capital, but would rather cut per capita capital in half – just as we are not born with a shovel in hand, we are not born with the ability to speak, to add or subtract, or to fly a Boeing 747. These require training. Romer operationalizes human capital as simply being “years of schooling” (a fuzzy correlate of “skills” writ large, but we must do the best with what we can), which is obviously something we invest in, just like we would tractors or steel mills or locomotive.

iii. And if we should change our assumptions?

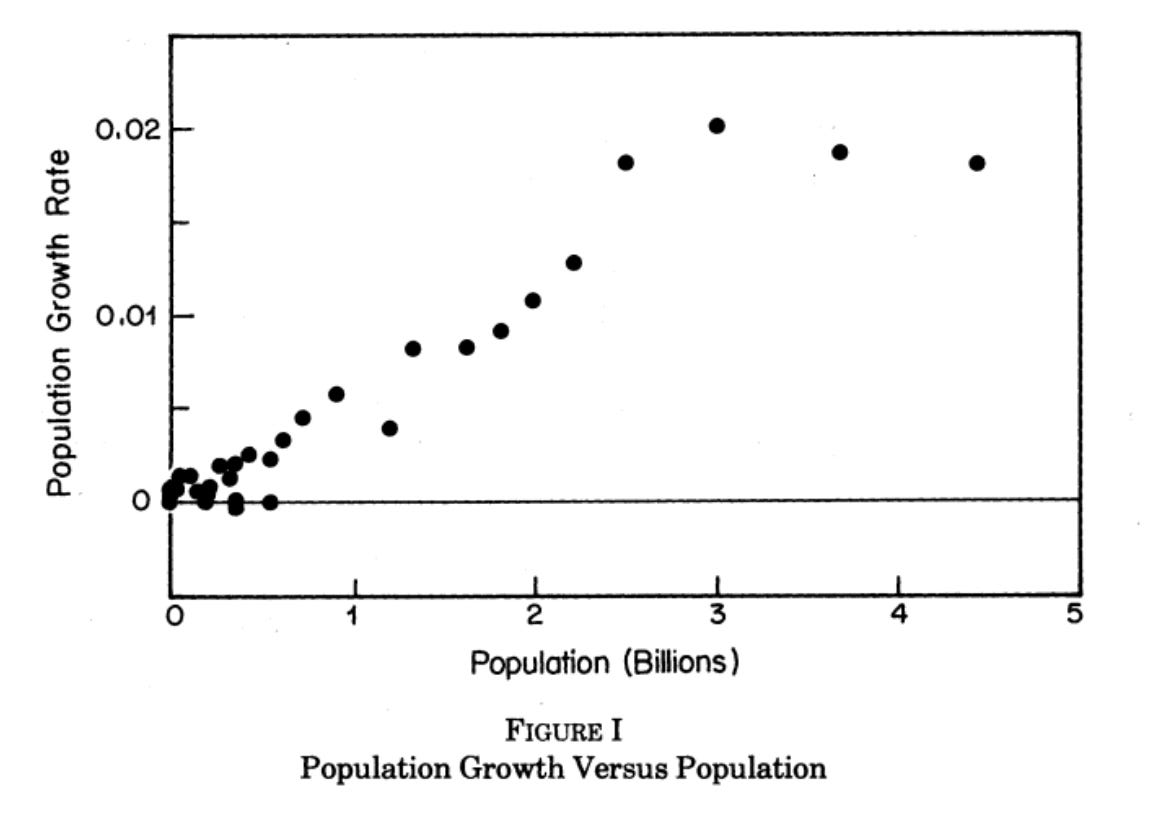
Kremer’s 1993 paper, “Population Growth and Technological Change: One Million BC to 1990”, makes a tiny change in the microfoundations and reaches radically different conclusions. In many ways we are born with the ability to speak. To acquire that knowledge is so trivially easy that it happens as if by accident. People are born helpless, but seek out skills instinctively. It is as if we are born with some amount of human capital, even if at the beginning we were but mewling infants. We can think of this as a non-linear cost of human capital in the Romer model. Once you break this assumption, suddenly population size matters. People randomly generate ideas, and the more of them there are, the more ideas you have. This is not to say that training does not matter, just that it isn’t all endogenous. He tests this simply, regressing population growth on population level.  In a Malthusian world, where income is simply arable land divided by the number of people, population growth will continue until no more people can be supported. Thus, while we cannot measure technology directly, we can infer its level from the number of people.

You can argue about the empirics of it – for example, in a Malthusian world, where income is simply arable land divided by the number of people, a model where innovation is sufficiently sensitive to wealth would overwhelm the effect of more people. This model originates from a Chad Jones paper in the 90s. Kremer is vulnerable to some criticism on a conceptual level – because we are using population to measure technological growth, it wouldn’t pick up a cultural change which led to individuals having fewer children than could be supported. Some of the early stories of why Europe industrialized relied on the European marriage pattern, which was women delaying marriage until later, and thus reducing the number of children they could bear. Income could be higher in Europe, particularly Northern Europe, than in the rest of the world, and tentatively (I do not wish to stir up the decades long hornets’ nest comparing real wage rates between country) they probably were. This is Eric Jones thesis, who wrote the foundational (read: first) book on the Great Divergence, The European Miracle. These stories needn’t contradict – all countries could have been at persistently suboptimal levels of saving, and the additional savings caused by the culture which also restricted fertility might overwhelm the invention story – but it is still troubling. You also predict that the Industrial Revolution would happen in China or India, not in Europe, where it did. In addition, any study based upon population estimates stretching back to 1500 – let alone to before the evolution of Homo sapiens — is going to not have good data. Kremer’s story still makes far more intuitive sense than Romer’s. But why should it matter? 

Once we assume that human capital is, to some degree, exogenously given, we can then reasonably assume that different people have different levels of human capital. Not everyone will attain the same amount. We can even go further, and not assume that the level of human capital — even after corrective subsidies to shift countries onto a higher steady state path — would, even in theory, be able to converge. The cognitive ability of a country could be exogenously given. Given that these differences persist even after immigration to higher ability countries, I think this is the most plausible explanation of IQ gaps between countries.

iv. IQ and Cognitive Ability

I want to differentiate “IQ” and “cognitive ability”. Cognitive ability is the underlying thing — IQ is the measurement. That our measure of it is fuzzy does not mean that the thing being measured is any less real, nor does it mean that it isn’t meaningful. Imagine a magical (and very defective) yardstick, which is sometimes six inches too long, and sometimes six inches too short, and sometimes anywhere in between the two. That you can never perfectly measure it does not mean that objects lack length. The length of an object or stretch of road exists independent of the tools we use to measure it. Neither does it mean using the yardstick isn’t useful. You must have confidence intervals, but you can say with some definitivity if something is pretty long, or something is pretty short. You can say with confidence that trees are tall, and mushrooms short, even if you aren’t sure exactly how tall they are. Nor does it matter if you measure something when the yardstick had shrunk a few inches one day, and grown a few inches the next day. You can say, “the height of that tree is 10 yards, give or take a yard” and that gives a very clear idea that it is meaningfully different from the tree which is 13 yards tall!

In order to test ability, we need to measure things which are learned in society. Because cognitive ability is in a very real sense “ability to learn”, this is fine — you show your ability to learn by learning things! We will never have the platonic ideal of an IQ test, and as a consequence we will never have a test which is provably totally unbiased with respect to what people learn. You can show that, controlling for scores on other questions, a particular question isn’t biased, but self-referentiality is impossible. What we can do is teach everyone the same material, and see how they do. Thus there is a sense in which all tests are IQ tests. It’s not just stuff which has “IQ test” on the tin, like the AFQT or Raven’s matrices. The SAT and ACT are intelligence tests; Regents is an intelligence test; the GRE and MCAT and LSAT are intelligence tests. If everyone is studying for it, and the test curved, then it gives us the same rank order of people by ability. There are people who study, and people who study less, but if this is perfectly correlated with ability there will actually be no effect on the rank-order or scores, and if not perfectly correlated, would only introduce some noise. 

v. On the weakness of educational attainment 

I have predicated the prior remarks on testing on everyone learning the same material. There is thus room for advancements in human ability from schooling. Michael Kremer’s other 1993 paper, “The O-Ring Theory of Economic Development”, forcefully makes the case that countries can be stuck in low-equilibriums of educational attainment, and low levels of skill. If the returns to your job are dependent upon what skills other people are getting, then you don’t get the full return, and consequently underinvest in education, compared to the social optimum. What good is learning how to be a software engineer, in a world where no one knows how to use a computer at all? These skills can be much more abstract than CS, of course — manipulation of shapes and symbols might be informed by practice with them in preschool. But we cannot take it too far. We cannot assume that simply increasing years of education will increase actual skill and ability. 

1. Years of education is itself endogenous to cognitive ability. Cross-country differences in educational attainment may simply represent actual differences in ability, not sub-optimal equilibria. If this is the case, then all we can do is try our best to raise the level of ability, and to not allow them to be stuck in bad institutional equilibria; but we cannot expect simply raising school years to have a society wide impact. This seems to be less the case in the developing world, though I would absolutely believe it to be the case as years of schooling approaches the Western norms.

2. Some of the private return to education may be signaling. We cannot then assume that our micro estimates will scale up into the macroeconomy. Two common designs for studies evaluating the effects of education, especially in the developing world, are randomized controlled trials, or a natural experiment taking advantage of an exogenous shock or quasi-randomness. The difficulty is showing that the gains for the treated group are due to an improvement to themselves, and are not parasitic upon the untreated group. Studies estimating the macro effects find much weaker effects than what would be implied from simply multiplying the treatment group up to the size of the whole population. A key study here is by Esther Duflo, on when Indonesia embarked on a massive school-building program. Children who got schools did better, and the initial paper considered it a success — but a later look showed that the wages of people who didn’t get a school fell. The net effect was still positive, but nowhere near as big as you might naively hope. It would also be highly implausible, if people are gaining more knowledge, that there were spillovers in productivity onto other workers. Romer 1986 is based entirely on this! Yet, at least on the margin in the US, there are no such spillovers. Acemoglu and Angrist used changes in the minimum age before you could drop out of high school, and differences in that between US states, to estimate the effect of one additional year of school on co-workers. They didn’t find anything. Now, yes, this is in America, and only to students who were on the brink of being high school dropouts. This is still the best we got — these questions are hard!

3. The skills learned may be specific and not generalizable. There is no evidence that “learning to learn” works. There’s no magical way to “develop your brain”, except perhaps that reading enables you to acquire information on your own. Learning another language makes you better at that language; it does not make you better at learning unrelated subjects. Ditto for learning the violin. The apparent correlation between the two is entirely spurious — parents who are smart and care about success have children who are smart and care about success. It is “confounded”, in other words.

People attend far more school now than they did in the recent past, but it’s not clear that this translates to economic growth. England had very little formal schooling during the Industrial Revolution, but also had the greatest density of “mechanics and millwrights”, as Mokyr would say, needed to implement other people’s inventions. The steam engine would be useless if you could not make a sufficiently fine gear. Implementing ideas is dependent upon the average of the whole population, not a few scattered geniuses, although the normally distributed nature of intelligence makes these the same. 

vi. Whence cognitive ability?

And where does cognitive ability come from? This is not especially scientifically controversial (with caveats), but it is controversial in the public eye. A great deal more heat than light has been generated. The causes of intelligence, as with any behavior or physical trait, are affected by genes and environment. Do not think, by the way, that environment means parenting! It is not! In fact, parenting has only a very small effect on a child’s outcomes. Environment is simply an error term, incorporating everything not explicitly explained by genes. The “heritability” of a trait is simply what percentage of the variation in traits is explained by genes; we should not expect this this to remain constant in all environments. Imagine a world where clear eyesight is perfectly heritable, and if you can’t see well, you can’t read. The invention of eyeglasses means that an entirely inherited trait is solved with environmental interventions. Two groups of plants, which are watered different amounts, might have all variation within the group be explained by genetics, and all variation between the groups explained by environment. 

One way to study the effects of genes is a twin study. Contrary to popular perceptions, this is not where identical twins are separated at birth. Rather, they are comparing the difference in variance between identical and fraternal twins. Identical twins are identical: fraternal twins share half their genome, no more than brothers or sisters. (You’ll often drop brother-sister sets of fraternal twins). The point of using fraternal twins, instead of any old set of siblings, is to control for environment — presumably, you were brought up in pretty similar ways, and anyhow, it wouldn’t systematically differ in the level of similarity of environment. One must adjust for assortative marriage, which will bias estimates of heritability up (because the fraternal twins are more similar to each other than we expected). These find estimates of the heritability of cognitive ability in excess of .5. Related, in the sense of not requiring knowledge of the genome, and thus runnable before the genome was sequenced, are adoption studies. This is just looking at the intelligence of adopted kids, as compared to their parents. I really don’t trust them, however — most adoptions are not clean handoffs at birth, the sample sizes are generally small, and the population isn’t random either. (An aside — you do need to control for IVF making twins more likely, and IVF usage is positively correlated with income).

There are also genome-wide association studies (or GwAS). These have only become available more recently, as they use large datasets containing whole genomes, like UK biobank data, to associate specific variants with traits of interest. They find much lower estimates than twin studies on the heritability of intelligence. Genes can interact with the environment. Genes can cause a difference in the past, which leads to a spurious association in the present — to take a toy example, imagine pollen allergies are perfectly heritable, and people with the pollen allergies move to the city. The plant dies out, but the association between pollen-allergy-genes and remains, in what is called a passive gene environment interaction. When traits are the results of many genes interacting, even sample sizes in the hundreds of thousands may be insufficient to determine causality. It can be very difficult to tease out whether something is inherited due to genes, or due to bits of culture which are passed along within families too. GwAS is concerned only with the direct causal impact of genes. Finally, much of the reason why they would differ from twin studies are violations of the equal environment assumption — identical twin environments are more similar than fraternal twins are. But all of our policy levers — income, education, and so on — are the same in twins. The source of environmental differences must be totally unknown to us. It is for that reason that I believe the policy relevant heritability of intelligence is high. It doesn’t matter whether it is literally the genes or not — if it is passed down in families, and we don’t know how to change it, it might as well be heritable. 

We should expect all differences in ability to become exaggerated over time, too. This is what is called a gene-environment interaction. Imagine two students, who differ only a small amount in innate ability. One of them finds reading natural, starts reading at an early age, and because of this, seeks out reading books. As they seek out books to read, they become better and better until they eventually max out. Another student finds reading more frustrating. If they kept practicing, they would eventually draw near the more gifted student, but they do not wish to practice. The gap, small in the beginning, widens to a chasm. This is how genes might only have a small direct effect on cognitive ability, but meaningfully “cause” a much larger portion of gaps in ability. (Clever readers will note the similarity between this, and Romer’s model of growth! Differences in initial conditions can lead to large differences in income).

We might expect culture to work this way too. Kids who aren’t doing so well in school disdain the utility of book knowledge, precisely because they are bad at it. Would it be any surprise that a group of them would look down upon anyone who was doing well? Mightn’t that discourage people from aspiring toward all they are capable of? Mightn’t this be the origin of the epithet “acting white”? And wouldn’t we expect institutions to be the same? All too often, good institutions are games of trust. We must believe we won’t be backstabbed in order to have democracy at all. To not have corruption, people must believe that enough people will act altruistically to punish wrongdoers, and not take bribes themselves. No one wants to be the only poor sap not taking bribes. Smarter people are more trusting and more cooperative, and have wider moral spheres. It is perfectly reasonable for small differences in human capital to have very large impacts on outcomes, and not just through changing the incentives for research.

vii. Rescuing Kremer

Thus, we can rescue the Kremer model, and reconcile it with restricted fertility. Human capital, remember, is taken to be, in part, effectively exogenous. Yes, everyone starts with zero skills, but some have a far easier time acquiring them. If the European marriage pattern — or anything else in the environment, how we got to the state of the world we are in hardly matters in the slightest for what we should do now — was selecting for abilities which later become much more relevant, then the economic world today is the relic of natural conditions thousands of years ago. Size of population does matter, but you have to weigh it by the ability to innovate of any of its residents.

There is quite sound evidence for this selection occurring. Greg Clark documents in his book “A Farewell to Alms” how wealthier people had more children over a very long period of time in England. In China, a similar correlation between living standards and income existed, according to Hu (2023). And in very recent papers, there was substantial selection amongst West Eurasians toward greater intelligence, among other traits, within the past six thousand years. Of course, the next step is to show that this trend wasn’t happening elsewhere. That it was occurring in the places we know now to be the smartest is necessary, but not sufficient, to show that it matters. This is the edge of science — I hope for much progress on this front. We economic historians have greatly underrated the role of intelligence in economic development, insofar as we have done very little to investigate it.

viii. What is to be done?

I want to end with reasons for hope. No matter your interpretation of human capital acquisition, we have every reason to think the world will continue to get better. Ideas found in America benefit the whole world. The world will be dragged along by the work of our best and brightest, just so long as the institutions in those countries allow the ideas to be used. 

We cannot take innovation for granted, though. We will never be at the optimal level of knowledge creation without government intervention. This is not a blanket call for more government, as much of what it does is either bad, or has nothing to do whatsoever with innovation. We should still have more funding of scientific inquiry. According to Nordhaus 2004, the inventor captures just 2.2% of the social surplus of an invention. Is there any world in which we get the optimal amount of effort, when we subject something to a 97.8% tax? It is difficult, when one thinks of the magnitude of lost innovations, to think that anything else comes even close to mattering as much. We should be willing to accept inefficiency in research. We should be willing to accept the funding of things we think are a bit silly. What matters more than anything else is shifting more resources to research, instead of present consumption.

We may never be able to shift poor countries onto a higher growth path. They may never be able to grow on their own, from their own ideas. That’s okay, so long as we, in the first world, do the work of generating ideas.