On Equilibrium in Voting and in Product Markets

With several theoretical problems posed

A frequent result in voting theory is that there is no need for a stable equilibrium to exist. This can happen for several reasons. For instance, you could have three voters trying to divide up a dollar between them. For every agreement between two players to divide it, there is another which defeats it. If Player A proposes to Player B that they split the dollar 50:50, then Player C can counteroffer to either that they split it 49:51, and so on.

The first person to first describe this was the Marquis de Condorcet, who showed that simple majority rule with a minimum of three people could lead to cycles. Three voters have the preferences, respectively, A>B>C, B>C>A, and C>A>B. A will always beat B, but will then lose to C, who will in turn lose to B. The group cannot truly be said to have a preference over the candidates.

We can think of each issue as a dimension. Voters have preferences over those issues, and vote for whichever candidate is closest to them. What is going on is that if we put the candidates on a line, one of the voters no longer has a single peaked preference. Thus we cycle between candidates, and the agenda setter decides the group’s decision.

Now, for single issues, we have some good news. If we posit that voter preferences are concave, then no paradoxes exist. If the issue is, for instance, an optimal tax rate, then if there are no people who prefer both a high or low tax rate to a medium rate the policy chosen will be the one favored by the median voter.. Candidates seeking to beat each other will converge to the same point, in what is called the median voter theorem.

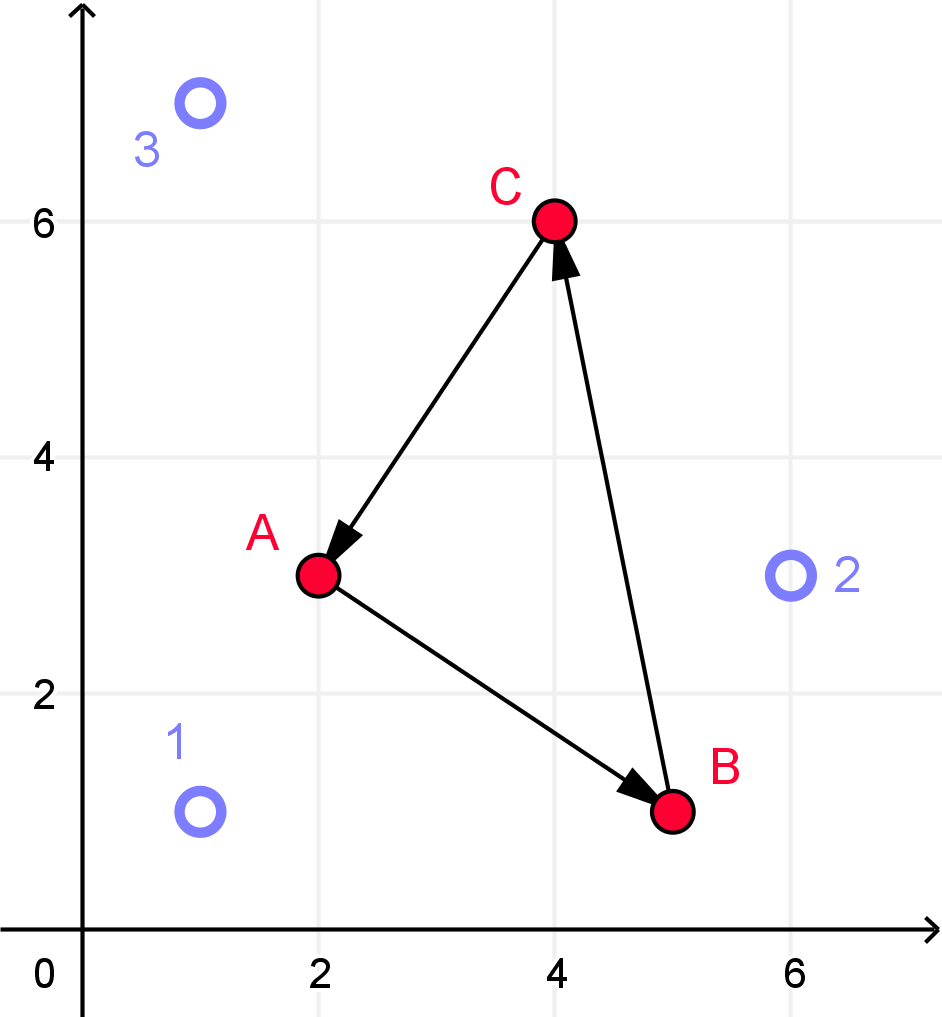
The problem is that once you add a second dimension, no such regularity exists. We cannot guarantee that an equilibrium will exist, even if every voter’s preference is concave. This is called the McKelvey-Schofield theorem. The Condorcet paradox mentioned above can be represented graphically down here, in an illustration I unashamedly borrow from Wikipedia.

Suppose that there are three clusters of voters which form an equilateral triangle in the issue-space. We shall assume that utility for society is given by finding the point which minimizes the squared distance from each voter. (It could be linear, but in a linear regression it would mean the intercept is indeterminate. So, I’ll just say quadratic). Assuming that all voters care equally about their positions, the socially optimal candidate would be at the center of gravity. However, this candidate would be beaten by one in any direction away from the center, and that candidate could in turn be beaten by another.

The model I laid out for thinking about issues was originally developed for thinking about the characteristics of products offered by firms by Harold Hotelling. In the Hotelling model, with a uniform distribution of buyers and no transport costs the firms converge to a single point. What concerns me is that, with no cost to switch characteristics, limited entry, and distinct clusters of consumers, no equilibrium exists. Firms can always find a set of characteristics which increases their profits.

Suppose that entry into a market is restricted so that there are only two firms, A and B. As before, they face three equally sized clusters of buyers. The socially optimal positions, since we can select two points, are for Firm A to place itself in one cluster, and the other, B, to place itself between the two clusters. However, Firm A would be reducing their profits if they did this. They could move to take more of the profits, but this would simply leave Firm B able to steal it back. There is no end to the cycle.

I think that this model, while extremely stylized, gestures toward something important about products. Why is it the case that fashion changes so often? Why is it the case that websites change their designs all the time? Why do fast food restaurants change their products all the time? Better explanations may exist, but this is at least worth contemplating.

I would also like to pose some problems which I contemplated, but could not solve. I would like to know how primaries work. Alright alright, I know how primaries work in practice, but what about in theory? Suppose there are two parties, which we’ll call R and D. One of them, R, has its position given exogenously. Perhaps it’s the incumbent. Party D needs to pick a candidate who will beat Party R’s candidate, conditional upon the Party D nominee being an improvement. How do they arrive at a candidate? If the process is the same, then we will need to figure out how voters coalesce around certain candidates. The process will be completely driven by arbitrary beliefs, and can support any outcome.

I think the way out is a mixed strategy Nash equilibrium, where candidates pay the fixed cost to enter if and only if they have the ability to win the general, and the ability to win the primary conditional upon the strategies of everyone else who could possibly enter. I do not know how to solve this.

We also have the problem that every voter is strictly better off casting a vote in every election they can. What would make this problem more reasonable is if I could state conditions under which there is a core of R voters who will never vote for a D candidate who meets the conditions of being able to beat the R candidate and being an improvement over the R candidate. I also do not know how to do this. You could do it very simply by saying that voters pay a fixed cost to vote, and so changing far away party priorities to be slightly closer is inconsequential. Strategic voting shows up here, though. Swinging the election is an enormous deal. Also, paying fixed costs makes it difficult to show it is rational for all but one person to vote.

This blog post has been a bit rambly. If I make any progress on the problems I laid out, you will hear it here first. Till then, your views are warmly welcomed.