What Do Economists Do?

A whirlwind tour of methodology

We are interested in what will happen in the future. In order to make accurate predictions, we have to know what caused what. Economics is a set of tools to answer questions of causality, attached to a set of theories to guide us as to what questions are worth answering. In this essay, I will show you how economists think about questions, the methods they use to identify causality, and how they can then use that causal evidence to answer much bigger questions.

We should start with ordinary least squares regression. It is the workhorse of economic analysis, and is the basis for most of the methods we will see later. Suppose that we have a sample of people, and we observe their years of education and their income. Since we think that years of education is causing the outcome, income, we place years of education on the X axis, and income on the Y axis. Income is given in logs, which will mean that, given a linear relationship of education and income, each additional year will increase income by a fixed percentage (rather than by a fixed amount). I have created some examples of what I am talking about in R. It will look something like this.

We can obviously draw a line which best approximates the data, which we generally do using ordinary least squares. In this, we choose the line which minimizes the summed up squared distance of each point from the line. Note that this is the vertical distance from the line, not the euclidean distance. (Using the euclidean distance would bias the slope if you measure the outcome with noise).

It looks like this. We can see that the line of best fit is positive. We can think of this as a simple equation, Income = A + B(x) + e, with e representing error. “A” is the y-intercept, and B is a coefficient which tells us how much a year of education increases income by. R-squared is a measure of how much of the variation the regression line explains (and is out of 1).

We choose the squared distance because if we did not, we would actually be totally indifferent to many different lines. If we shifted the line upwards, keeping the slope the same, the total distance from the line would actually stay the same. Intuitively this is because the distance from the line, positive and negative, must always sum to 0. Squaring is useful. We don’t want to have higher powers, because that would make it excessively influenced by outliers. There are some other advantages as well – absolute value isn’t differentiable, so if we’re trying to minimize the difference, we can’t just take the derivative of everything and solve for 0. See this reddit thread for more, as I had to go looking this up myself.

Of course, this is merely a correlation. In order for us to argue that education causes the increase in income, we have to argue that there are no factors which correlate both with the number of years of education and later income. For example, perhaps smarter people both take more years of education, while also being more skilled while in the labor market, but without the education affecting either. For this, we need to turn to our toolkit of methods.

We could try and control for intelligence directly. We compare outcomes only within a certain level of IQ, and then estimate the effect of a year of education. However, this is obviously inadequate. Intelligence might be correlated with other things which we cannot measure, which will affect both years of education and earnings, like attentiveness or work ethic. On top of that, intelligence might be affected by education, and is thus a mediating variable for the effect of education on income. If we control for this, then we will spuriously get no relationship. Alternatively, intelligence might affect the years of education sought, and through that channel, affect income. In short, “controlling for observables” is almost never going to do what we want it to do, and is something of a tell for a study being somewhat sloppy and unserious. Instead, we have to use other methods.

The simplest and cleanest is randomization. We have a pool of people, some of whom we assign at random to receive more of the treatment – in this case, education – than others. If our randomization is uncorrelated with people’s characteristics, then we can find the true effect. For example, suppose some people are assigned at random to go to high school, while others are not. If the people who are otherwise identical but sent to high school for four years earn 40% more than the people who were not, and only had 8 years, we can infer that a year of education increases income by 10%. This is called a randomized controlled trial, and is commonly used for testing medicine.

We can generalize this to cases where we are not in control of the procedure ourselves, using two-stage ordinary least squares. We need an instrumental variable (z), which satisfies the conditions that it is correlated with x, but is not correlated with e. We can break apart x in the equation before into x = p + x(hat)z + v, where p is the intercept, x(hat) is the coefficient which is correlated with z, and v is the error as before. X(hat) is exogenous, so now we can use that instead in the regression, Y = A + Bx(hat) + e. An example of an instrumental variable might be a program which randomly assigns a scholarship to students to go to college. Some students will choose to not go to college, even with the scholarship, so using 2sls (this is the ordinary abbreviation for two-stage least squares) lets us answer this.

These instrumental variables can be really quite clever. One of my favorite examples is from Justine Hasting and Jesse Shapiro (2018) who are interested in what people spend SNAP benefits on. (SNAP is the successor program to food stamps). When someone becomes certified as eligible for food stamps, they remain eligible for six months, unless they show that they remain eligible. This results in people eligible for intervals which can be divided cleanly into six months. If someone got a job three months in, and becomes no longer eligible, then they will suddenly and discontinuously lose their benefits three months later on, which is uncorrelated with changes in their underlying circumstances. Using this, they can infer that people substantially increase their spending on food when they are paid in food stamps, which is a bit of a surprise – if the total amount of SNAP benefits is less than what they normally spend on food, then it should be no different from cash.

Of course, we’re still rarely going to observe a source of randomization as clean as that of a randomized controlled trial, or the assignment of scholarships as before. The exogeneity of the instrument is a fundamentally untestable assumption – we need to make an argument that it is plausibly uncorrelated, but we can never actually prove it.

One of the great examples of plausibly arguing for exogeneity comes from the two mammoth papers on the effects of neighborhoods from Raj Chetty and Nathaniel Hendren. (I link the original draft, which combines the two into one, for convenience). They want to estimate how much of the later-life outcomes of children is due to the characteristics of the children, and how much is due to the place they live in. Obviously, we cannot simply regress the characteristics of the neighborhood on outcomes, because the place where people choose to live is endogenous. They have three basic methods of attack. First, families move as a unit. If a family has three kids, ages 2, 4, and 6, and they remain in a neighborhood until all of the kids are 18, then they will receive 16, 14, and 12 years of exposure to the new neighborhood. If the younger children see a larger convergence to the income of the new neighborhood, we can infer that this indeed due to the neighborhood.

Next, they identify large outflows from ZIP codes, which might be the result of a hurricane or a factory being closed. They do a two-stage least squares using the average quality of neighborhood that people affected by the common shock to account for sorting, and find that the convergence pattern they found with the family fixed effects method is still there. They argue for the strength of their instruments using “placebo tests”. Specifically, they note three patterns, which are difficult to explain except through the neighborhoods actually affecting children’s outcomes. First, neighborhood outcomes change over time, and people converge to their own birth cohorts, and not others. Second, they look at the distribution of outcomes. Their example for this is Boston and San Francisco, which have similar average outcomes, but with San Francisco having higher variance. Third, they look at differences between genders. Men and women have different rates of convergence given observed characteristics of a neighborhood, and families which move with a child of the right gender do see larger or smaller rates of convergence.

You can never totally prove that the places that people chose to move to were uncorrelated with their expectations about future outcomes, and the investments that they intend to make in their children. However, you can argue that it would highly implausible for it not to be exogenous, and hope for your arguments to carry the day.

Other methods that we can use include a regression discontinuity design. Here we are making an assumption that the characteristics of the population of interest are smooth, but that there is a sudden jump – a discontinuity – at some point. Suppose that, to return to education, there is a test to advance to the next year. If you score below a threshold, you are held back, and receive one more year of education. If you score just above the threshold, you are advanced to the next year. All we have to do is assume that the underlying capabilities of people are smooth as their test scores increase, and we can infer the effects of a year of education (on the people close to boundary. Another common example of regression discontinuity in practice is from elections. Suppose there are many referendums in a state on whether the local school district should pursue build a new school. Places where the referendum fails to pass 49-51 are likely very similar to places where it passes 51-49.

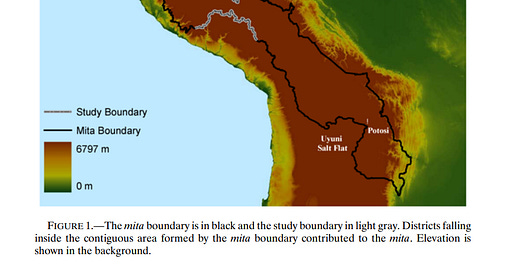
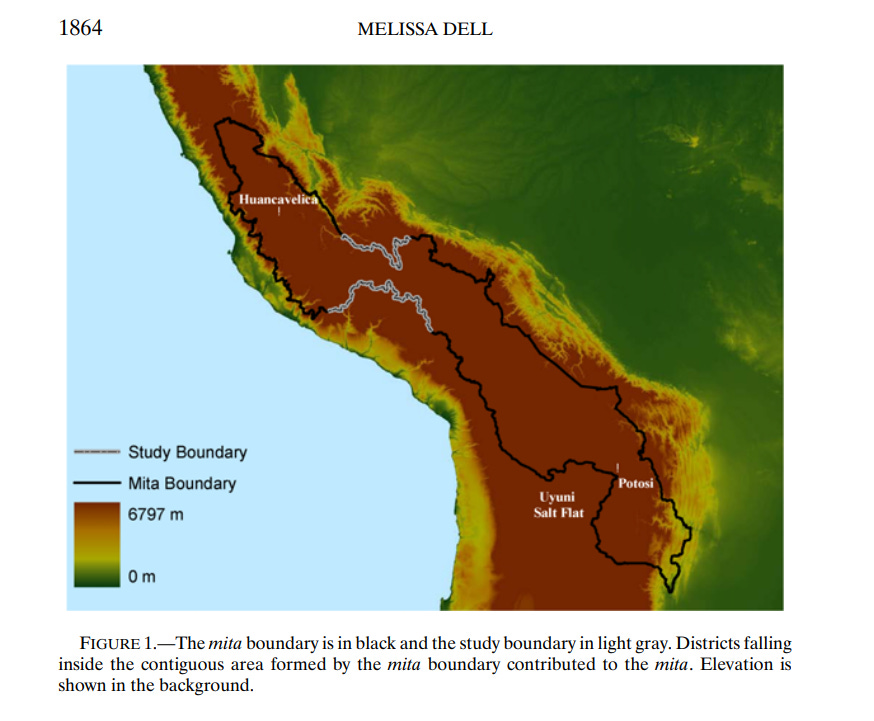
Regression discontinuity in action looks like Melissa Dell’s 2010 paper “The Persistent Effects of Peru’s Mining Mita”. The “mita” was a system of forced labor which the Spanish imposed upon their conquests in the former Incan empire. Illustrated here are the boundaries of the mita system – outside the black line, the indigenous were exempt. If the lines are arbitrarily drawn through a region whose characteristics are otherwise not arbitrarily changing, then you have plausibly exogenous variation. As you can see in the image, much of the line parallels the edge of the mountainous region. It is quite plausible that the characteristics of residents change discontinuously with altitude. In the highlighted region, however, the line cuts arbitrarily through the mountains. Altitude and ethnic mix are the same on each side, and the census taken in 1573 right before the mita was imposed show no systematic differences with the segment. Thus, she can argue that the later worse outcomes for the places with the mita are due to the mita, and nothing else.

Often times economists find plausible candidates for using regression-discontinuity design through knowing the quirks of a system. For example, in California, newborns are allotted a minimum number of two days of care, which are measured not as 24 hour periods, but as any midnight in care. Thus, a newborn born a few minutes after midnight will receive one more day of care than someone born just a few minutes before. Almond and Doyle (2011) use this quirk to estimate the effects of a day of hospital care, and find that there is no benefit to health of staying in the hospital a day longer for uncomplicated births. This is awesome! We’ve shown people how we could save billions of dollars at no cost to patients!

Another method commonly used – and which is, in fact, the most common method in applied empirical economics – is called difference-in-differences. The key assumption here is that the treated and untreated group, even if their characteristics were different, were going to have parallel trends. Take a hypothetical tutoring program, which is given to a worse performing set of schools than those who receive no tutoring. If the gap between the two narrows, we can infer that this is due to the program if we grant the assumption that they would not have otherwise narrowed the gap.

Alternatively, we can do what is called triple differences, and measure the change in the rate of change. Now we can have groups that are growing at different rates, and see whether their growth rates change. An example of this in practice is Banerjee and Duflo (2014), who are studying the effects of an Indian program expanding lending subsidies. They believe that firms are credit constrained in the developing world, which implies that if they suddenly got access to credit, they will expand production. Unconstrained firms would simply substitute it for other sources of borrowing. Firms were growing all the time, but what they can measure is the change in the rate of growth.

A conceptually similar approach to difference-in-differences is the shift-share method. Suppose that there are a number of regions, which each specialize in different industries to different degrees. One commuting zone might have a lot of steel plants, while another makes carpets, and another ceramics. Now suppose, as in Autor-Dorn-Hanson (2013), you’re interested in the effect of import competition from China. Suppose China gets better at steel, but not at making carpets. They use exports to other developed countries to infer what is due to China getting better at producing, and what is due to other stuff. From this, they can find the labor market impacts of import competition.

Care must be taken, in all three of the cases discussed above, that you are appropriately weighting your sample size. Things are related to themselves, and so are not actually independent observations. If something occurs in space, like Dell’s paper, we could get significance by dividing up the land into arbitrarily small units. Alternatively, if the effects take place over time (as in Banerjee and Duflo) we can spuriously increase significance by taking many measurements. This problem is discussed in Bertrand, Duflo, and Mullainathan (2004), with the solution being to cluster observations together. I refer the reader to the original source for more information.

Thus far we have been discussing “partial equilibrium” estimates, where we are comparing the difference in outcomes between affected and unaffected groups. In order to find the “general equilibrium” effect, we have to make some assumptions, or make a more extended argument. One is the stable unit treatment value assumption, or SUTVA. Essentially it’s just “no spillovers”. If one group is treated, then it doesn’t affect the untreated group. Suppose we’re trying to estimate the effects of education, and the treated group tutors the untreated group to bring them up to speed. Clearly, education does increase income, but we can’t measure it.

A more realistic example of this is from Esther Duflo, who was following up on her earlier paper on school construction in Indonesia. In the first paper, she used school construction as an instrumental variable to estimate that receiving one more year of education increased wages by about 6% per year of education. However, people having more education changes the labor market as a whole, such that it can depress wages for people who didn’t receive education. This will lead us to overstate the gain from education. Note that there is nothing fundamental about this result, and the bias could totally flow in the other direction – suppose that education made people into better managers, who then raised the productivity of uneducated workers. In that case, we would underestimate the true effect of education on wages. Relatedly, Duflo, Dupas, and Kremer (2021), in evaluating a program which randomly assigned scholarships to secondary schools, found that income gains to recipients came from having more government jobs. It’s plausible that those jobs are rationed, and so by taking one it worsens the jobs which untreated individuals can get. A partial equilibrium increase is consistent with a general equilibrium decrease.

So what can we do with our well-identified evidence? Sometimes, as in many of the papers we looked at here, the evidence is interesting for its own sake. However, we can go one step forward, and use this to parameterize a model. We would like to be able to say something about counterfactuals which we have not actually observed. To do this, we write down a model of the world, which boils down outcomes into a few parameters, which we can then plug in values that we find using the methods discussed before.

Let’s use one of my favorite papers ever, “Railroads of the Raj”, from Dave Donaldson. He wants to know what the effect of infrastructure was on incomes in British colonial India. A standard method would simply be to argue that there were these lines which came close to being built, but never were, and then compare treated and untreated regions. This method would find that incomes did indeed increase considerably in areas which got railroads.

This simple method leaves us in the dark, though, about why incomes increased. Maybe it was simply due to troop movements along the route that brought additional investment. Maybe governance improved due to better communication, or increased attention paid, or due to them getting better administrators. Maybe they received news earlier about technological improvements and were more likely to adopt them. In order to know what the effect of other transportation improvements would be, independent of any of the suggested things which might correlate with the railroad, we need to know how much of the income gains from the railroad are gains from trade. To do this, you need a model.

The model in question is from Eaton-Kortum (2002). In order to make it tractable, we do need to make a plausible assumption about how productivities are distributed. Once we grant this, the way forward is clear. He measures trade costs from the prices of varieties of salt which are produced in only one region but are marketed nationally. He estimates the elasticity of expenditures in a district on goods sourced internally from rainfall shocks, and with that in hand, he can show that gains from trade can be given entirely from regional productivity and the share of expenditures which are sourced from outside the district. Gains from trade due to the railroad were responsible for half of the increase in income.

Or, to give another example, we want to know how far from optimal allocation we are. To know this, we need to know the markup of firms, or the difference between price and marginal cost. We don’t observe marginal cost, so we need some way to estimate it. Now, we thankfully do have an answer. Given some production function, with output being a function of fixed inputs (like a factory) and variable inputs (like labor and materials), cost minimization implies that the Lagrangian is marginal cost. So, we can find the markup by looking at the elasticity of output with respect to the variable input, divided by the elasticity of the variable input’s share in revenue. Intuitively, if output increases by 15%, and the variable input’s share of costs increases by 10%, the difference between this is the markup – markup is 50% over marginal cost. We need to know what the production function is first, though. To do this, we need to use instrumental variables, as before. Generally, the assumption is that the fixed input is a function of past productivity, which is exogenously determined by market demand.

To sum up, economics is about making predictions. To do this, economists make models of the world, and then estimate the parameters in those models.